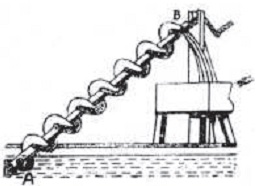
Another important invention was the screw pump, made by an important mathematician and inventor named Archimedes. As the screw is turned (and there are many variations of this design), water is raised up and eventually pours into the elevated container.
Also attributed to Archamedes was the principle of displacement, which you can see in the image below. The precise volume of something, in this case a bolt, can be discovered by measuring how much liquid it displaces… that it pushes aside.
Archamedes realized that this explains how boats float upon water:
If the weight of the boat is less that the weight of the water it displaces, it will float.
If the boat weighs more than the amount of water is displaces, it will sink.
The Depth of Mathematics
As we noted back in Lesson 4, several Greek mathematicians and philosophers began to grasp not only that they could define a large number of mathematic laws, but that the world itself operated by mathematics.
One of these mathematicians, named Euclid, very carefully proved one axiom (a very precise statement) after another, building a very strong foundation for mathematics. And he did this using lines, circles, diameters, triangles and so on… he proved things true with geometry.
Here, for example are the shapes he used to prove the Pythagorean theorem of right triangles:
And here’s the construction and proof of an equilateral triangle, using two equal circles:
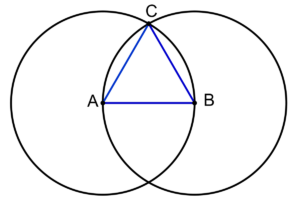
In the end, Euclid and others proved that the inner structure of the universe could be described with mathematics… that the universe itself functioned by mathematics. Some of the Greeks went a bit wild with these ideas, but the truth is that mathematics does underlie the entire physical universe, and that’s worth being excited over.
A New Base
The technologies put in place by the end of the Roman era created a new technological base: a very large set of technologies that allowed for a broader range of experiences and development. Through much of the world, especially including the West (Europe and nearby areas), people understood that tremendous things were possible to them. They knew this because they had seen it done (aqueducts, immense numbers of trading ships coming and going and so on), and in very many cases they had been part of it themselves. After all, it wasn’t the rulers who built ships, sewer systems and conducted trade, but working people.
Even as Rome fell apart, and certain technologies were no longer maintained (the system of Roman roads, for example), very little technical knowledge was actually lost, and people didn’t forget what they had done. As we’ll see in the next lesson, immense building projects continued, as did nearly all the knowledge that had been gained over the years.
END
LESSON PLAN
As always, go slowly and be sure the students understand the lesson as completely as possible.
When teaching this lesson in particular, be prepared to take significant tangents. One thing can easily lead to another with this material, and the curiosity of children is to be cultivated, not ignored. Even if you can’t get to their interest right away, make a show of writing it down and assure them that you’ll get back to it; give them a fixed date if at all possible.
If this lesson takes two or three times as many days as the others, let it, and please use as many tools and practical demonstrations as possible. These things matter, and people forget that even the greatest and most abstract scientists began with very practical, hands-on demonstrations. Albert Einstein, for example, was raised in the electrical shop of his dad and uncle, who were busy installing the first electric street lights in the city of Munich.
Demonstrate Euclid’s way of deriving an equilateral triangle from two circles. All you’ll need is paper, a pen, a compass and a ruler. You can find plenty of demonstrations to work from. Do the Pythagorean theorem also if you can. Show them some pages from Elements and let them see how he made his proofs.
I also suggest that you take a day to examine the Pythagorean theorem and at least one practical application, such as measuring the height of a tree or building. It’s important for students to see such things working in real life, and to do it with their own hands and eyes. This will also give you a strong opportunity to teach the concept of squared numbers, or even cubed numbers if the students are grasping squares and seem not to be out of energy. Simple children’s play blocks will work quite well for this.
When explaining the displacement image, please add that the ∆V (delta-V) in the image stands for “change in volume,” with ∆ (the Greek letter delta) signifying change and V signifying volume.
If the students have some interest in “Greeks going too far” with mathematics, please spend a bit of time examining the Pythagoreans: it’s an interesting and enigmatic story, including some fairly silly things, like refusing to eat beans. (No one is sure why.)
Again I’ve italicized new and significant words. You may want to spend time on these with your students:
Accrete.
Irrigate.
Crops.
Geometric (art).
Wrought.
Axiom. (And again I suggest that you read a few from Elements.)
Displacement.
Volume.
END